Цикл Карно

 

Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.

 

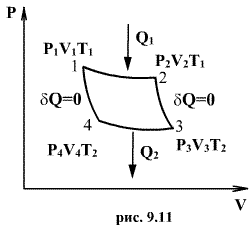
При изотермическом расширении от нагревателя отбирается тепло  (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны P₂V₂T₁ . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т₂. Параметры точки 3 – P₃V₃T₂ . На участке 3-4 газ изотермически сжимается. Параметры точки 4 – P₄V₄T₂ . Выделяющееся при этом тепло Q₂ отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту Q₁ , а холодильник отобрал Q₂ Разность Q₁-Q₂ определяет полезную работу газа за один цикл, так как согласно I началу термодинамики δQ=δA+dU , но для кругового процесса dU=0 и, следовательно δQ=δA .

Отношение полезной работы к затраченной энергии нагревателя определяет коэффициент полезного действия (к.п.д.) тепловой машины:

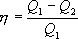 (9.23)

Эта формула справедлива для любого обратимого и необратимого процесса.

 

Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу Q₁=A.

Тогда

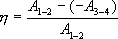
или

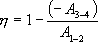
Для изотермического процесса работа

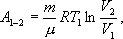
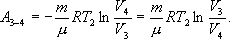
С учетом последних выражений

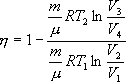 (9.24)

Покажем, что

 

 

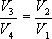
Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между V₁ и V₂ и V₃ и V₄ используем уравнение Пуассона в виде TV^r-1=const

Следовательно,

T₁V₂^r-1= T₂V₃^r-1

и

T₁V₁^r-1=T₂V₂^r-1

Разделим эти уравнения и получим

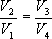
Тогда выражение для к.п.д. (9.24) примет вид

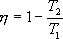
Эта формула справедлива только для обратимого цикла Карно.

 

Теоремы Карно.

Все обратимые машины, работающие по циклу Карно, имеют, независимо от природы рабочего тела, одинаковый КПД при условии если у них общий нагреватель и холодильник.

Если две тепловые машины имеют общий нагреватель и холодильник и одна обратимая, а другая необратимая, то КПД обратимой больше необратимой