Энергия волны

 

Найдем изменение энергии малого объема dV упругой среды, связанное с распространением в среде плоской волны, которая задана уравнением

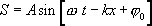 (8.9)

Ввиду малости объема dV можно считать, что все находящиеся в нем частицы среда колеблются в одной фазе, так что их скорости одинаковы и равны

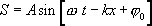
Поэтому кинетическая энергия объема среды dV, связанная с колебательным движением, равна

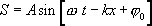
где ρ - плотность среды. Из (8.9) следует

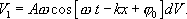
Поэтому

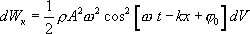 (8.10)

Подсчитывая работу деформации объема dV среды при волновом движении (деформация сдвига в случае поперечной волны и деформации объемного сжатия в случае продольной волны), можно показать, что потенциальная энергия dWп объема dV среды равна его кинетической энергии. Полная механическая энергия dW колебательного движения элементарного объема dV упругой среды равна сумме его кинетической и потенциальной энергии.

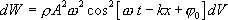 (8.11)