Момент инерции материальной точки относительно неподвижной оси вращения
Согласно второму закону Ньютона, для тангенциальной
составляющей силы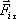 
, действующей на материальную точку массой m, и
ускорения
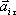
можем записать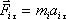
С учетом, что
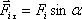и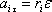 
Имеем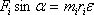 
Помножим левую и правую части на 
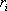и получим 
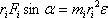(5.2)
или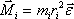
Произведение массы материальной точки m1 тела на квадрат ее расстояния ri2 до оси вращения называется моментом инерции материальной точки относительно оси вращения:
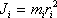(5.3)
,
