Момент инерции твердого тела

 

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

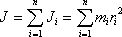(5.4)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами dm, и моменты инерции тела определяется интегралом

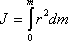  (5.5)

где r - расстояние от элемента dm до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью плотности 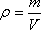  (5.5)

где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение дает среднюю плотность.

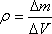
Плотность в данной точке в этом случае определяется следующим образом

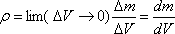
и тогда 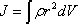 (5.6)

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

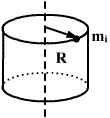
Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

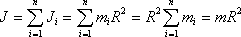
Сплошной однородный диск. Ось вращения является осью диска радиуса R. и массы m с плотностью 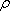 Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки dr и массой dm. Для него

dJ=r²dm

Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

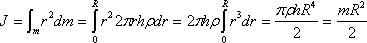
Момент инерции шара относительно оси, проходящей через центр тяжести.

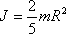
Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня -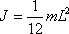

б) через начало стержня -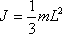

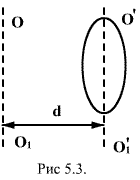
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс O₁’O’ известен. Необходимо определить момент инерции относительно произвольно оси OO₁ параллельной оси O’O₁’. Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями: 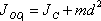 (5.7)