Рассмотрим диэлектрическую пластинку, заполняющую плоский конденсатор (рис.14.5) и находящуюся, следовательно, в практически однородном внешнем поле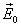 
.
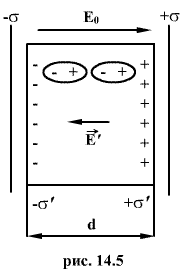
В результате поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей окажутся нескомпенсированными соседними диполями. Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, окажется избыток положительного заряда с некоторой поверхностной плотностью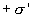 
. На противоположной стороне диэлектрика 
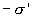. Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекул диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению дополнительного электрического поля 
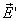, направленного против внешнего поля 
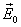. Результирующее электрическое поле Е внутри диэлектрика равно
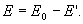(14.2)
Для определения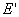 
применим формулу вычисления напряженности 
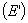конденсатора
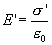(14.3)
Свяжем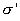 
с вектором поляризации Р. Для этого определим полный дипольный момент (во всем объеме) диэлектрика. Осуществим это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
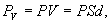(14.4)
где S - площадь пластины конденсатора.
С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряд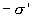 
, а с другой 
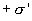и расстояние d. Отсюда
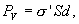(14.5)
Приравнивая (14.4) и (14.5), получим
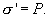
Подставляя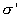 
в (14.3), и затем результат в (14.2), получим
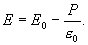
Подставим значение Р из выражения (14.1), тогда
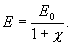(14.6)
Величина
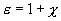(14.7)
называется диэлектрической проницаемостью или относительной диэлектрической проницаемостью. Диэлектрическая проницаемость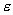 
показывает во сколько раз уменьшается напряженность в диэлектрике по сравнению с напряженностью в вакууме. 
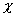и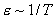 
, т.е. с ростом температуры диэлектрические свойства ухудшаются.
,
