Пусть проводник заряжен с поверхностной плотностью заряда σ.Рассмотрим небольшую цилиндрическую поверхность, образованную нормалями к поверхности проводника и основаниями dS, одно из которых расположено внутри, а другое вне проводника. Поток вектора электрического смещения через эту поверхность равен
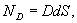
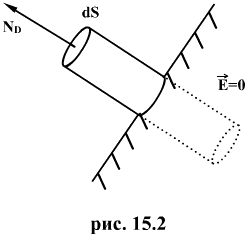
Где D - величина смещения в непосредственной близости к поверхности проводника. Действительно, поток через внутреннюю часть цилиндрической поверхности равен нулю, т.к. внутри проводника 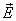 , а значит и
, а значит и 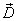 , равно нулю. Вне проводника в непосредственной близости к нему напряженность поля
, равно нулю. Вне проводника в непосредственной близости к нему напряженность поля 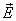 направлена по нормали к поверхности проводника. Следовательно, для выступающей наружу боковой поверхности цилиндра
направлена по нормали к поверхности проводника. Следовательно, для выступающей наружу боковой поверхности цилиндра 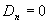 , а для внешнего
, а для внешнего  . Внутрь цилиндра попадает свободный заряд
. Внутрь цилиндра попадает свободный заряд 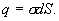 Применяя к цилиндрической поверхности теорему Гаусса, получим
Применяя к цилиндрической поверхности теорему Гаусса, получим 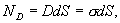 , т.е.
, т.е. 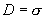 . Отсюда для напряженности поля вблизи поверхности проводника получаем
. Отсюда для напряженности поля вблизи поверхности проводника получаем
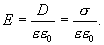 (15.1)
(15.1)
В общем случае распределение зарядов зависит от формы проводника и должно быть таким, чтобы создаваемое им внутри проводника поле удовлетворяло условиям 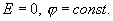 . Но вследствие взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга, что и приводит к скоплению зарядов на более удаленных концах. Отсюда следует, что и плотность зарядов на выступах велика.
. Но вследствие взаимного отталкивания заряды стремятся расположиться как можно дальше друг от друга, что и приводит к скоплению зарядов на более удаленных концах. Отсюда следует, что и плотность зарядов на выступах велика.
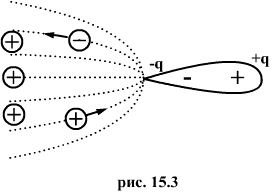
Особенно велика бывает плотность зарядов на остриях. Поэтому напряженность поля вблизи остриев может быть настолько большой, что происходит ионизация молекул газа, окружающего проводник. Ионы иного знака, чем q, притягиваются к проводнику и нейтрализуют его заряд. Ионы того же знака, что и q , начинают двигаться от проводника, увлекая с собой нейтральные, молекулы газа. В результате возникает ощутимое движение газа, называемого электрическим ветром. Заряд проводника уменьшается, он как бы стекает с острия и уносится ветром. Поэтому такое явление называют истечением заряда с острия.



