Как было показано выше, отношение 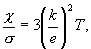Произведенные Лоренцем, уточненные расчеты с учетом классического распределения по скоростям привели к замене в теоретической формуле множителя 3 на 2 и к резкому увеличению расхождения теории с опытом. Второе затруднение классической электронной теории возникло при сопоставлении с опытом формул для теплоемкостей. Согласно электронной теории теплоемкость единицы объема электронного газа равна 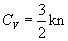, где n - концентрация свободных электронов. Теплоемкость, отнесенная к одному электрону, 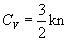. Рассмотрим один кг - атом одновалентного металла. Он состоит из 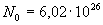ионов, колеблющихся около своих положений равновесия, и 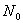свободных электронов. Колебательная теплоемкость твердого тела по закону Дюлонга и Пти равна 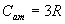, теплоемкость электронного газа

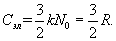
Следовательно, по электронной теории теплоемкость одновалентных металлов должна составлять 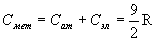. Однако опыт показывает, что теплоемкость металлов так же, как теплоемкость твердых диэлектриков, в соответствии с законом Дюлонга и Пти близка к 3R. Таким образом, обнаружилось неожиданное и непонятное явление практического отсутствия теплоемкости у электронного газа.

Третьим затруднением классической электронной теории металлов явилась невозможность правильно объяснить с ее помощью температурную зависимость сопротивления. Опыт показывает, что сопротивление металлических проводников линейно возрастает с температурой по закону

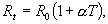
т.е. проводимость обратно пропорциональна абсолютной температуре в первой степени: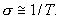

Согласно классической теории, проводимость обратно пропорциональна 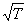. Наконец, возникли трудности при оценке средней длины свободного пробега электронов в металле. Для того чтобы, пользуясь формулой (18.3), получить такие значения удельной электрической проводимости металла, которые не расходились бы с опытными, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, приходится предположить, что электрон проходит без соударений с ионами решетки сотни межузельных расстояний. Такое предположение непонятно в рамках классической электронной теории Друде -Лоренца.

Приведенные выше противоречия указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.