Одновременность событий в разных системах отсчета

Пусть в системе K в точках с координатами x₁ и x₂ происходят одновременно два события в момент времени t₁=t₂=t. Согласно преобразованиям Лоренца в системе K’ этим событиям будут соответствовать координаты

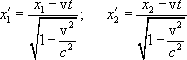
и моменты времени

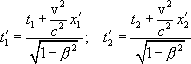
где

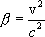
Из написанных формул видно, что в случае, если события в системе K происходят в одном и том же месте пространства (x₁=x₂), то они будут совпадать в пространстве (x’₁=x’₂) и во времени (t’₁=t’₂) также в системе K’.

Если же события в системе K пространственно разобщены 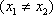, то системе K’ они также окажутся пространственно разобщенными 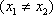, но будут одновременными. Знак разности (t’₂-t’₁) определяется знаком выражения v(x₁-x₂). Из этого следует, что в разных системах K’, (при разных v) разность (t’₂-t’₁) будет различна по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Сказанное относится только к событиям, между которыми отсутствует причинная связь.

Причинно связанные события (например, выстрел и попадание пули в мишень) ни в одной системе отсчета не будут одновременными и во всех системах событие, являющееся причиной, будет предшествовать следствию.