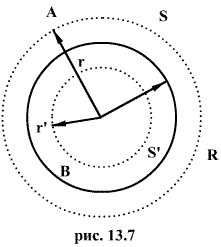
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 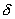 заряда в любой точке сферы будет одинакова.
заряда в любой точке сферы будет одинакова.
-
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
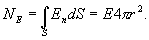
По теореме Гаусса
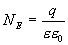
Следовательно
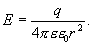 (13.8)
(13.8)
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
-
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
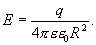 (13.9)
(13.9)
-
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е.
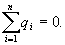 Следовательно, по теореме Гаусса,
Следовательно, по теореме Гаусса, 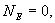 и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.
и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.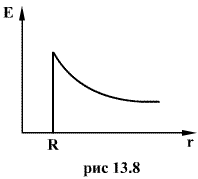
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью . 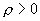
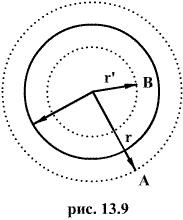
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда 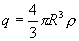 , расположенного в центре шара. Тогда вне шара
, расположенного в центре шара. Тогда вне шара
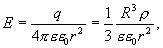 (13.10)
(13.10)
а на его поверхности (r=R)
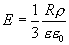 (13.11)
(13.11)
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 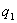 , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
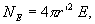
с другой стороны, в соответствии с теоремой Гаусса
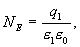
Из сопоставления последних выражений следует
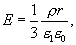 (13.12)
(13.12)
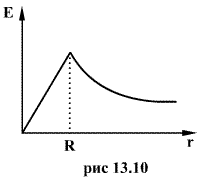
где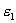 - диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
- диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью 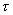 .
.
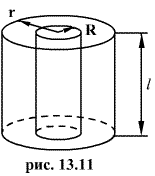
Проведем коаксиальную цилиндрическую поверхность радиуса 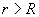 Поток вектора напряженности через эту поверхность
Поток вектора напряженности через эту поверхность
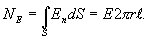
По теореме Гаусса
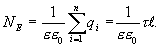
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
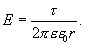 (13.13)
(13.13)
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен ?. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
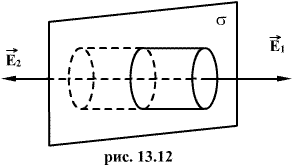
Суммарный поток вектора; напряженности равен вектору 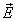 , умноженному на площадь S первого основания, плюс поток вектора
, умноженному на площадь S первого основания, плюс поток вектора 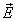 через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,
через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом, 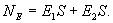 С другой стороны по теореме Гаусса
С другой стороны по теореме Гаусса
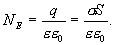
Следовательно
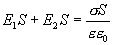
но 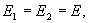 тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
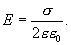 (13.14)
(13.14)
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
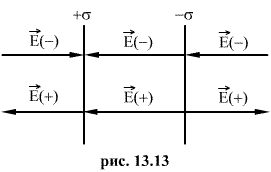
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов 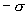 и
и 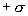 , равны сумме напряженностей полей, создаваемых пластинами, т.е.
, равны сумме напряженностей полей, создаваемых пластинами, т.е.
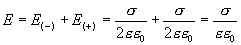
Таким образом,
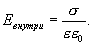
Вне пластины векторы 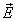 от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.