1.5. Скорость

 

Для характеристики движения материальной точки вводят векторную физическую величину - скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.

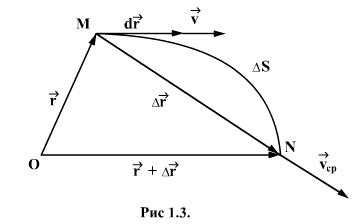
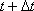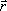Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени  в т. N. Радиус-векторы точек М и N соответственно равны , а длина дуги МN равна 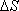 (рис. 1.3).

 

Вектором средней скорости 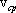 точки в интервале времени от t до t+Δt называют отношение приращения  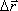радиуса-вектора точки за этот промежуток времени к его величине 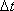: 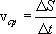(1.5)

 

Вектор средней скорости направлен также, как вектор перемещения 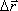 т.е. вдоль хорды МN.

 

Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя 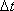 к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории. 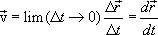 (1.6)

 

В процессе уменьшения величины 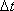 точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектор 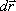 и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат. 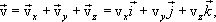 (1.7)

 

 

где 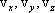 проекции вектора скорости на оси координат х, у, z.

 

Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим: 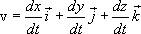(1.8)

 

Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки: 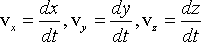> (1.9)

 

Поэтому численное значение скорости: 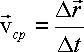(1.10)

 

Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.

 

Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.

 

В этом случае часто пользуются скалярной величиной 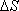, называемой средней путевой скоростью неравномерного движения на данном участке 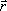траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути 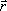 затрачивается то же время 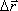, что и при заданном неравномерном движении: 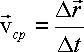 (1.11)

 

Т.к. 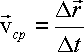 только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае: .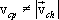

 

Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения 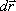 в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности: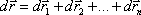

 

В соответствии с определением (1.6): 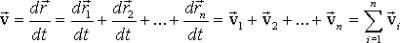(1.12)

 

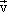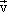Таким образом, скорость  результирующего движения равна геометрической сумме скоростей  всех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).