Связь между потенциальной энергией и силой 

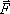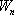Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

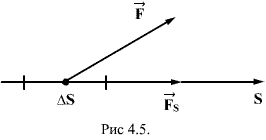
Для установления этой связи вычислим элементарную работу ∆А, совершаемую силами поля при малом перемещении ∆S тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой S. Эта работа равна

∆А=F_sdS

где F_s- проекция силы 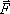 на направление S.

 

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии W_x’, она равна убыли потенциальной энергии –W_x’ на отрезке оси ∆S:

∆А=–W_x’

Из двух последних выражений получаем

F_sdS=–W_x’

Откуда

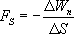
Последнее выражение дает среднее значение F_s на отрезке ∆S. Чтобы получить значение F_s в точке нужно произвести предельный переход:

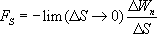
Так как W_x’ может изменяться не только при перемещении вдоль оси S, но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от W_x’ по S:

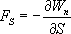
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

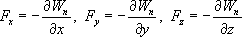
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

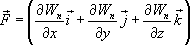в математике вектор ,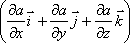

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символ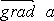ом . Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком 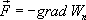  (4.15)