Уравнение плоской волны распространяющейся в произвольном направлении
Получим уравнение плоской волны, распространяющейся в
направлении, образующем с осями координат х, у, z углы α,β, γ
Пусть колебания в плоскости, проходящей через начало координат, имеют вид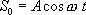 
.
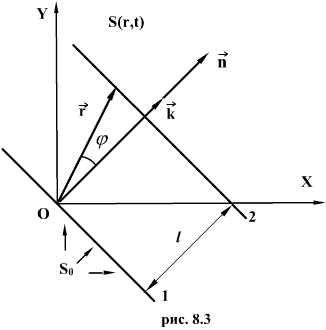
Возьмем волновую поверхность (плоскость), отстоящую от начала
координат на расстоянии l. Колебания в этой плоскости будут отставать от
колебаний в точке О (рис.8.3) на время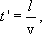 
тогда уравнение волны
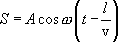(8.4)
Выразим расстояние l через радиус-вектор точек
рассматриваемой поверхности. Для этого введем единичный вектор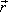 
нормали к волновой
поверхности. Скалярное произведение
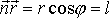
Подставим значение l в уравнение (8.4) и внесем в скобки
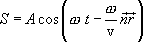
Отношение 
равно волновому числу k. Вектор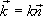 
равный по модулю
волновому числу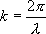 
и имеющий направление вдоль нормали к волновой
поверхности называется волновым вектором. Введя вектор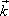 
, получим
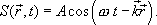(8.5)
Чтобы перейти от радиуса - вектора точки к ее координатам х,
у, z , выразим скалярное произведение 
через проекции векторов на координатные оси :
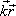
Тогда уравнение плоской волны принимает вид:
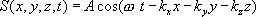(8.6)
где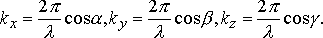 
>
,
