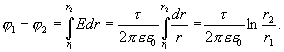1. Электрическое поле сферической поверхности радиуса R.
-
Разность потенциалов между двумя точками, лежащими на расстоянии
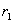и 
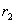от центра заряженной сферической поверхности 
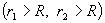, находим из формулы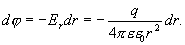
Интегрируя левую и правую части этого уравнения
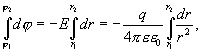
получим
-
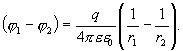
Положив
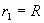и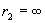 
, получим потенциал заряженной сферической поверхности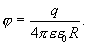
-
Внутри заряженной сферы поля нет, и потому весь ее объём эквипотенциален, т.е.
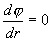и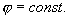 
и равен потенциалу на поверхности (при r=R).
2. Потенциал электрического поля плоскости.
Найдем разность потенциалов между двумя точками М и N, лежащими на расстояни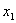и 
и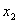 
от плоскости. 
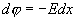, Но для плоскости 
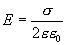, поэтому
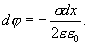
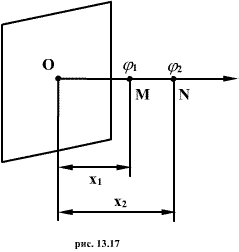
Проинтегрировав последнее выражение по х от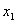 
до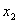 
и обозначив потенциал в точках М и N через 
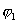и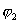 
, получим
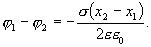
3. Разность потенциалов между двумя параллельными плоскостями
Находящимися на расстоянии а друг от друга, найдем аналогичным путем:
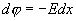, или (с учетом 13.15)
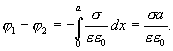
4. Электрическое поле бесконечного длинного прямого кругового цилиндра.
Воспользуемся, как прежде, связью потенциала с напряженностью и уравнением (13.13):
,
