Для любой точки внутри проводника напряженность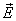 
результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил 
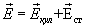. Подставляя в (17.6), получим
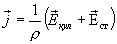
Умножим скалярно обе части на вектор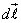 
, численно равный элементу 
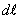длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока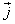 
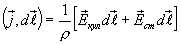
Так как скалярное произведение совпадающих по направлению векторов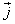 
и 
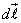, равно произведению их модулей, то это равенство можно переписать в виде
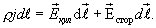
С учетом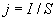 
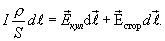
Интегрируя по длине проводника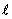 
от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем
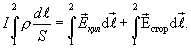(17.7)
Интеграл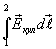 
численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что
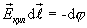
Таким образом,
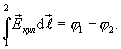
где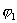 
и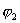 
- значение потенциала в т.1 и т.2.
Интеграл, содержащий вектор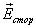 
напряженности поля, сторонних сил, представляет собой эдс 
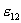, действующей на участке 1-2
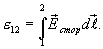(17.9)
Интеграл
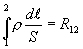(17.10)
равен сопротивлению участка цепи 1-2.
Подставляя (17.10), (17.9) и (17.8) в (17.7), окончательно получим
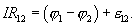(17.11)
Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической энергии, включённых на участке.
При замкнутой внешней цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей внешней цепи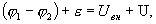 
где 
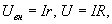или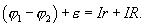 
Отсюда
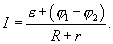(17.12)
,
