При рассмотрении кинетической теории газов и закона распределения Максвелла предполагалось, что на молекулы газа не действуют никакие силы, за исключением ударов молекул. Поэтому, молекулы равномерно распределяются по всему сосуду. В действительности молекулы любого газа всегда находятся в поле тяготения Земли. Вследствие этого, каждая молекула массой m испытывает действие силы тяжести f =mg.
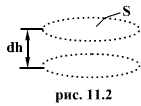Выделим горизонтальный элемент объема газа высотой dh и площадью основания S (рис. 11.2). Считаем газ однородным и температуру его постоянной. Число молекул в этом объеме равно произведению его объема dV=Sdh на число молекул 
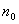в единице объема. Полный вес молекул в выделенном элементе равен
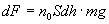
Действие веса dF вызывает давление, равное
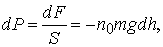(11.2)минус - т.к. при увеличении dh давление уменьшается. Согласно основному уравнению молекулярно-кинетической теории
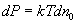(11.3)
Приравнивая правые части (11.2) и (11.3), получаем
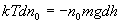или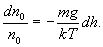
Интегрируя это выражение в пределах от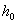 
до h (соответственно концентрация изменяется от 
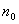до n):
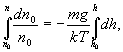получим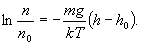
Потенцируя полученное выражение, находим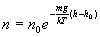
(11.4)
Показатель степени при exp имеет множитель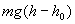 
, который определяет приращение потенциальной энергии молекул газа. Если переместить молекулу с уровня 
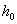до уровня h, то изменение ее потенциальной энергии будет
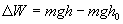
Тогда уравнение для концентрации молекул преобразуется к виду
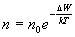(11.5)
Это уравнение отображает общий закон Больцмана и дает распределение числа частиц в зависимости от их потенциальной энергии. Он применим к любой системе частиц, находящихся в силовом поле, например в электрическом.
,
